The RSA algorithm, named after its inventors Ron Rivest, Adi Shamir, and Leonard Adleman, is one of the most widely used encryption methods for secure data transmission. It was developed in 1977 at MIT and is still a fundamental part of modern cryptography.
Unlike symmetric encryption, which uses a single key for both encryption and decryption, RSA is an asymmetric encryption algorithm. This means it relies on a pair of keys: a public key that can be shared freely and a private key that must be kept secret. While these keys are mathematically connected, knowing one does not reveal the other, which is what makes RSA so secure.
At the heart of RSA is number theory, particularly the challenge of factoring large prime numbers. The security of the algorithm comes from the fact that breaking it would require enormous computational power, making it practically impossible with current technology.
Thanks to its reliability, RSA is widely used in secure communications, protecting sensitive information exchanged between parties. Now, let’s take a closer look at how it works.
Key components of the RSA Algorithm
The RSA algorithm consists of several key components, including key generation, encryption, decryption, mathematical foundations, security considerations, and padding schemes. Each of these plays a crucial role in ensuring the algorithm's effectiveness and security.
Key Generation: RSA relies on a pair of keys: a public key for encryption and a private key for decryption. The public key is shared freely, allowing anyone to send an encrypted message to the intended recipient. The private key, however, is kept secret and is the only key that can decrypt the message. The strength of RSA lies in the mathematical relationship between these keys, which ensures security while allowing secure communication.
Encryption: In encrypting a message, the user uses the recipient's generated public key, to encode the message to be sent into a ciphertext (encrypted form of the original message), which only the receiver decrypts using his private key.
Decryption: Decryption is performed by the recipient using their private key, which converts the ciphertext back into its original plaintext form. Since only the recipient possesses the private key, unauthorized access to the message remains nearly impossible.
Mathematical Foundations: RSA’s security is rooted in number theory, specifically:
- Prime Factorization: The difficulty of factoring a large number that is the product of two prime numbers (p and q) is what makes RSA secure. If an attacker could factor this product, they could break RSA encryption.
- Modular Arithmetic: RSA relies on modular exponentiation, which is efficient for encryption and decryption.
- Euler’s Theorem: This theorem helps in efficiently computing large powers in modular arithmetic, playing a key role in RSA’s encryption process.
Security Consideration: The strength of RSA depends on the assumption that factoring a large composite number (n = p × q) is computationally infeasible with current technology. If an attacker could factor n, they could derive the private key from the public key, breaking the encryption. This is why modern RSA implementations use very large prime numbers to maintain security.
Padding Schemes: To enhance security, RSA uses padding schemes such as:
- OAEP (Optimal Asymmetric Encryption Padding): Protects against attacks like chosen plaintext and chosen ciphertext attacks.
- PKCS#1: A standard defining cryptographic message structures, ensuring secure encryption practices.
These padding schemes add randomness and structure to the message before encryption, preventing certain cryptographic attacks that could otherwise exploit weaknesses in plain RSA.
How does the RSA Algorithm work?
Now that you have learned about the components of the RSA algorithm, let's examine how it works.
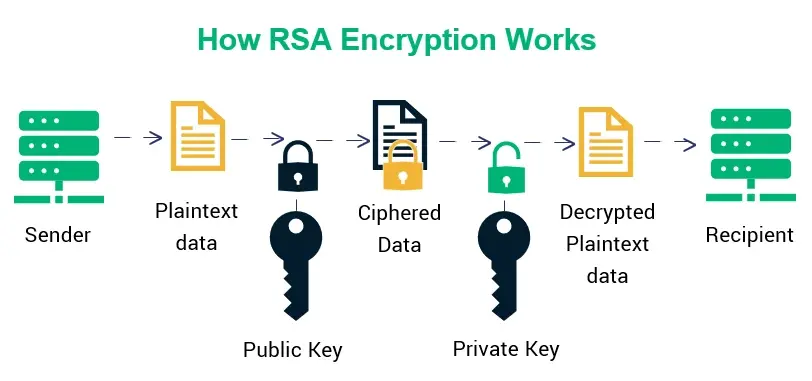
In systems where the RSA algorithm is applied, certain steps and procedures are followed internally to ensure secure communication. You can see the operational flow in the steps below:
Step 1: Selection of two (2) large prime numbers
This is the first step in the entire process; two (2) random prime numbers are generated independently of each other and secretly kept. The product of these two prime numbers is stored in a variable n, which is referred to as modulus.
This modulus n is used during encryption and decryption of a message. The modulus n can be represented mathematically as n = p x q. Where p and q are the large random prime numbers, take note of these characters, as we will be making references to them in the later parts of this article.
Step 2: Generation of the public and private keys
The second step concerns the generation of the public and private keys. The algorithm chooses an integer known as e to create a public key. The constraint for selecting the number e is that it must not be divisible by (p-1) or (q-1). From the first step, we already know that p and q are large prime numbers generated by the algorithm.
e is an important part of the public key, which is used for encryption. The pair of (e, n) makes up the public key. We should know by now that n is the product of p and q. The public key, as the name implies, is made public and available to anyone for use in sending an encrypted message to the receiver.
The private key, given as (d, n), is obtained by applying an inverse function over the e and (p-1)(q-1) to compute the value of d. The recipient is the only one who has this private key, for decrypting messages.
Step 3: Encryption
Here, the public key already generated in the second step is used to encrypt a plaintext message into ciphertext. The encryption step's goal is to ensure that only the recipient who possesses the private key can decode the ciphertext into the original message in its plain form.
Let’s quickly illustrate this using Python code for easy understanding.
# RSA Encryption: Convert Plaintext to Ciphertext
# Given values
M = 5 # Plaintext message
e = 7 # Public exponent
n = 33 # Modulus
# Encryption formula: C = (M ** e) % n
C = pow(M, e, n) # Efficient modular exponentiation
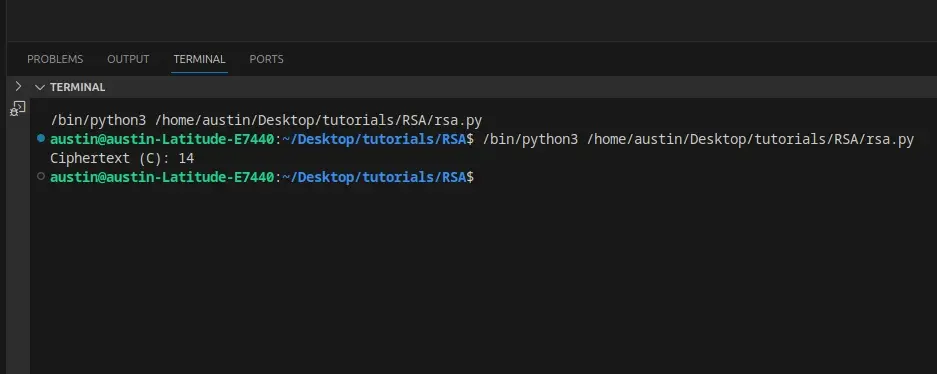
print("Ciphertext (C):", C)
The Python code snippet above shows us how encryption works on a lower level. M, our plaintext value of 7, was encoded to a ciphertext of value 14 using the encryption formula.
Note that in the code, C = pow(M, e, n) was used instead of C = (M e) % n** because of the computational benefit that it brings. The latter is not recommended because of the performance issues that accompany operations on large prime numbers.
By running the code, you should get this output:
Let’s move on to the last step.
Step 4: Decryption
The recipient of the ciphertext C then decrypts it to a plain text message M using the private key available only to them. It does so in the following steps:
- It computes the private key exponent d using this mathematical formula: d = e -1 mod ϕ(n!) where ϕ(n)=(p−1)×(q−1)
- Decryption is done using this mathematical formula: M = Cd mod n.
Let’s decrypt our encryption example using Python.
from sympy import mod_inverse
# Given values from encryption
C = 14 # Ciphertext obtained from encryption
e = 7 # Public exponent
n = 33 # Modulus
p = 3 # First prime number
q = 11 # Second prime number
# Compute φ(n)
phi_n = (p - 1) * (q - 1)
# Compute private key exponent d (modular inverse of e mod φ(n))
d = mod_inverse(e, phi_n)
# Decryption formula: M = (C ** d) % n
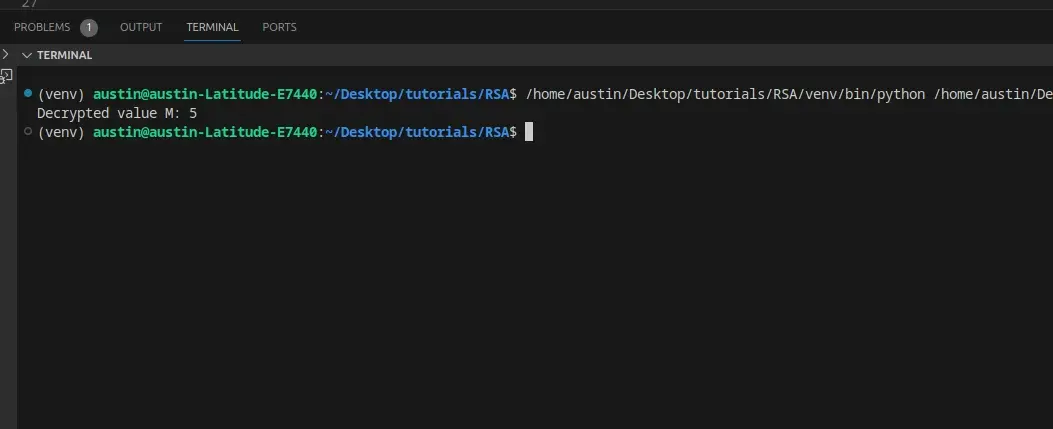
M = pow(C, d, n)
# Output the decrypted plaintext M
We just demonstrated decryption in RSA using the sympy library for mod inverse operation. After successfully running the code, the output should be the same as the image below:
Strengths and Weaknesses of RSA
RSA is a widely used encryption algorithm known for its strong security and versatility. However, it also has some limitations, particularly in terms of performance and potential vulnerabilities. The table below summarizes RSA’s key strengths and weaknesses:
| Strengths | Weaknesses |
|---|---|
| Strong Security – Based on the difficulty of factoring large prime numbers, making it resistant to brute force attacks with sufficiently long keys. | Slow Performance – Computationally expensive compared to symmetric encryption, especially with large key sizes. |
| Widely Adopted – Trusted and extensively used in protocols like HTTPS, PGP, and digital signatures. | Inefficient for Large Data – RSA is best for encrypting small amounts of data (like keys) rather than bulk encryption. |
| Secure Key Exchange – Enables safe transmission of encryption keys over untrusted networks. | Weak Key Management Risks – If the private key is exposed or stored improperly, security is compromised. |
| Supports Digital Signatures – Provides authentication and data integrity by allowing users to sign and verify messages. | Vulnerable Without Proper Padding – Without secure padding schemes (e.g., OAEP), RSA can be attacked through chosen-ciphertext methods. |
| Resistant to Most Classical Attacks – As long as key lengths are sufficient (e.g., 2048-bit or higher), breaking RSA with traditional computing is impractical. | Threatened by Quantum Computing – Future quantum computers could break RSA encryption using Shor’s Algorithm. |
Real-world applications of the RSA Algorithm
The RSA encryption algorithm has many real-world use cases. Let’s look at some of them below:
- Financial Transactions: We all know how important it is for financial transactions to be secure. RSA is incorporated into financial software applications to encrypt users' financial data, such as online banking or payment gateway systems.
- Cloud Storage Services: In cloud storage systems, RSA encrypts files for confidentiality, ensuring that only authorized users can access their contents.
- Digital Signatures: Digital signatures are created using RSA, ensuring authenticity and integrity with applications that access several use cases such as Document Signing, Software distribution, and Blockchain and Cryptocurrency.
- Secure Email Systems: For secure email communication, RSA is used to ensure proper encryption of emails sent across the Internet so that they can only be decrypted by the intended recipients.
Conclusion
Data Encryption algorithms provide a safe and secure way to send and receive information between computer systems by encrypting the message to be sent so that only the rightful recipient can decrypt and access its content.
Without data encryption systems, as is the case in most real-world applications and platforms, communications among computer systems would be insecure and bare.
In this article, we have learned about RSA's key components, strengths and weaknesses, and some of its real-world applications. Despite the speed bottleneck due to the generation of large keys, the RSA algorithm remains one of the most secure and widely used encryption algorithms.
Frequently Asked Questions
How do machine learning algorithms improve facial recognition applications?
Machine learning algorithms improve facial recognition by enhancing the accuracy and efficiency of recognizing and verifying faces. These algorithms use neural networks to process and analyze facial features from images and videos, learning from data collection to accurately identify individuals even under varying conditions.
How does algorithmic price discrimination affect the buyer-seller relationship?
Algorithmic price discrimination personalizes prices based on consumer preferences and willingness to pay, potentially strengthening the buyer-seller relationship by offering tailored deals. However, it can also harm the relationship if consumers feel that such price discrimination is unfair or exploitative, leading to a loss of trust and loyalty.
What are AI-powered trading algorithms and how do they impact crypto trading?
AI-powered trading algorithms use artificial intelligence to analyze market data, predict trends, and execute trades automatically. They help reduce human error and can respond to market changes much faster than manual trading, thereby potentially increasing profitability and efficiency in crypto trading.
What role does the object detection algorithm play in image recognition technology?
The object detection algorithm plays a crucial role in image recognition technology by determining the locations of objects within an image. It enables the image recognition model to label images by detecting and classifying objects, using methods like the region proposal network and faster region-based CNN to provide precise object localization.

Joel Olawanle is a Software Engineer and Technical Writer with over three years of experience helping companies communicate their products effectively through technical articles.
View all posts by Joel Olawanle




















